Damping Ratio Second Order System
Step Response Of A Second Order System With Respect To The Damping Download Scientific Diagram
Damping ratio second order system. The natural frequency ω is 565 rads and the damping coefficient ζ is 0707. The damping ratio and ringing frequency of a second order vibration measurement system is 005y8y500y0. If the Damping Ratio is equal to 1 then the system is said to be Critically Damped and if it is.
Small oscillation respor c. There are many ways of defining the order a system. Now natural damped frequency can be calculated as ω _d 11sqrt 1 -.
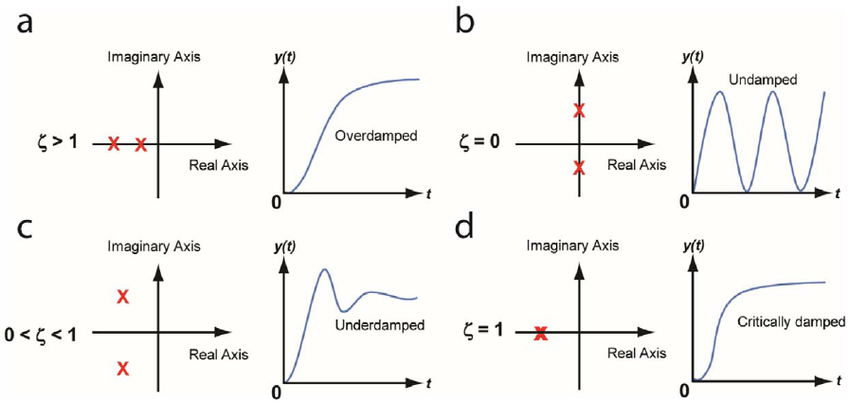
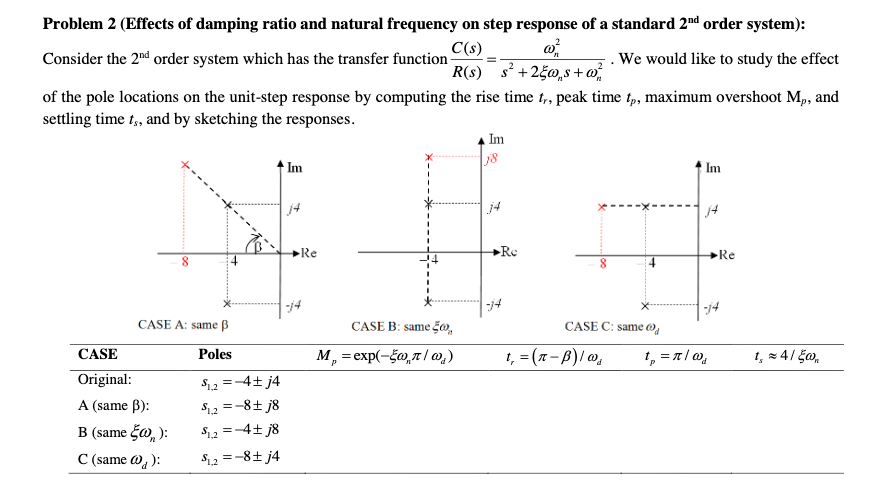
The damping ratio ζ is the ratio of the actual damping b to the critical damping bc 2 km. The system is underdamped. Question 3 The frequency response of a second-order prototype system is shown in Figure 7.
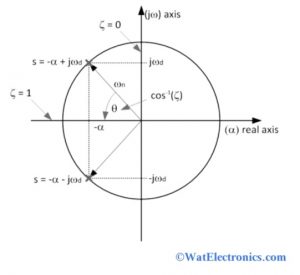
0 ζ 1 - underdamped system. If damping ratio is less than 1 then the system is called Under Damped. The pole locations are.
It is also the number of energy storage elements. A negative damping rate is not damping but driving. Follow these steps to get the response output of the second order system in the time domain.
General case for a second-order system. There is a standard and useful normalization of the second order homogeneous linear constant coefficient ODE mx bx kx 0 under the assumption that both the mass m and the spring con stant k are positive. ζ Damping ratio.
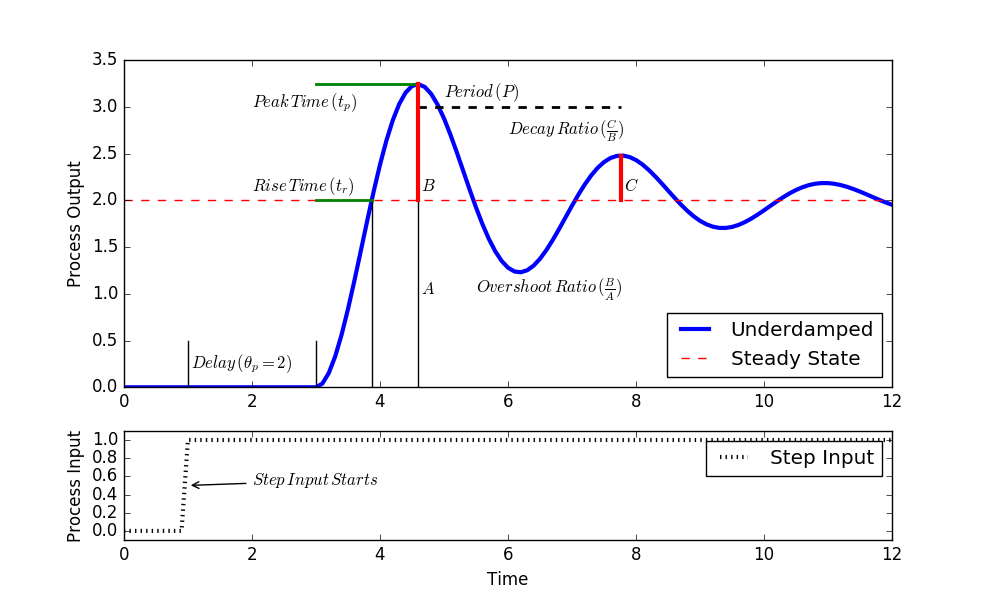
Settling Time The settling time is defined as the time required for the system to settle to within 10 of the steady state value. Here the relation between settling time bandwidth frequency and damping ratio is.
Intro To Control 9 3 Second Order System Damping Natural Frequency Youtube
Illustrating The Values Used To Derive Damping Ratio Of A Second Order Download Scientific Diagram
Chapter 5
Solved Determine The Poles Zeros Static Gain Damping Chegg Com
Control Systems Cs Lecture14 15 Time Domain Analysis
Damping Wikipedia
Help
2nd Order System Response
2nd Order System Dynamics
Time Response Of Second Order Control System Worked Example Electrical4u
Control System Solved Problem From Differential Equation Second Order System Calculate Damping Ratio Youtube
Step Response Of A Second Order System With Value Of Damping Ratio Less Download Scientific Diagram
Time Response Of Second Order Control System Worked Example Electrical4u
Automatic Control Theory Cse 322 Lec 7 Time
Time Response Analysis Of Control System Presentation Powerpoint Slides
Solved A Second Order System Has The Transfer Function G S Chegg Com
Lecture 13 Second Order Systems Time Response Lecture 12 First Order Systems Lecture 13 Second Order Systems Lecture 14 Non Canonical Systems Me 431 Ppt Download
Describe The Nature Of The Second Order System Response Via The Value Of The Damping Ratio For The Systems With Transfer Function G S 12 S 2 8s 12 G S 16 S 2 8s
Second Order Systems Dynamics And Control
Chapter 5
Graphical Method Second Order Underdamped Dynamics And Control
Engineer On A Disk
Solved Problem 1 Consider The Following Second Order System 1 X S S2 23 4 Calculate System Natural Frequency Nan System Damping Ratio C A Course Hero
1
Second Order Control System Response To A Unitary Step As A Function Of Download Scientific Diagram
Damping Ratio Wikipedia Republished Wiki 2
Alternative To Rlocfind To Find Intersection Of Line Of Constant Damping Ratio With Root Locus In Matlab Stack Overflow
Transient Time Response Of A Second Order Underdamped System With 0 D Damping Ratio 1
Second Order System Example 1
Solved A Second Order System Has The Transfer Function G S Chegg Com
Second Order System An Overview Sciencedirect Topics
Ebook Engineering Analysis Using Scilab And C
Solved A Second Order System Is Subjected To A Sinusoidal Input Undamped Natural Frequency Is 3 Hz And Damping Ratio Is 0 Calculate The Amplitude Course Hero
Second Order System An Overview Sciencedirect Topics
Second Order System Example 1
Time Response Of Second Order Systems
Time Response Of Second Order Control System Worked Example Electrical4u
Answered Second Order Control System Models One Bartleby
How To Find Damping Ratio Of A 4th Order System Electrical Engineering Stack Exchange
Damping Wikipedia
Harmonic Response
Determine The Damping Ratio ƹ Of The System From The Graph Quora
A Second Order System Has Damping Ratio X And Natural Frequency Wn The Unit Step Response Is
Step Response Of A Second Order System With Respect To The Damping Ratio Z The Poles Are Shown As X
Underdamped Second Order System Dademuchconnection
Problem 2 Effects Of Damping Ratio And Natural Chegg Com
Second Order System S Velocity Feedback Gain Control Based On Pid Variable Damping Ratio Controller Semantic Scholar
Damping Ratio In Control System Formula Its Significance
1
The damping ratio and ringing frequency of a second order vibration measurement system is 005y8y500y0.
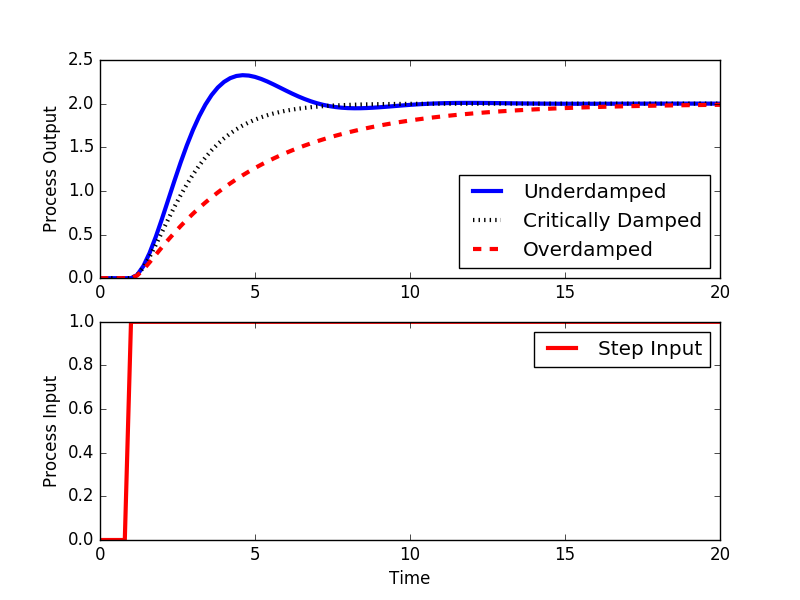
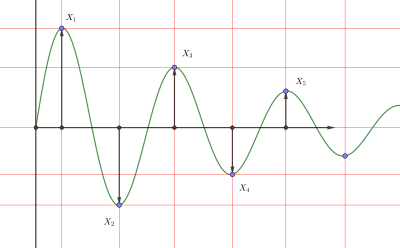
Follow these steps to get the response output of the second order system in the time domain. Question 3 The frequency response of a second-order prototype system is shown in Figure 7. Damping refers to dissipation of energy in a system. Equation 3 depends on the damping ratio xi the root locus or pole-zero map of a second order control system is the semicircular path with radius omega _n obtained by varying the damping ratio as shown below in Figure 2. 0 ζ 1 - underdamped system. The damping ratio is given by ζ cos θ. To derive the damping ratio in the control system or damping ratio in a closed-loop system consider the differential equation of the second-order system which is given as d2x dt2 2ζωn dxdt ωn2x 0. For critically damped continuous time second order system roots of denominator are. The response of the second order system mainly depends on its damping ratio ζ.
The pole locations are.
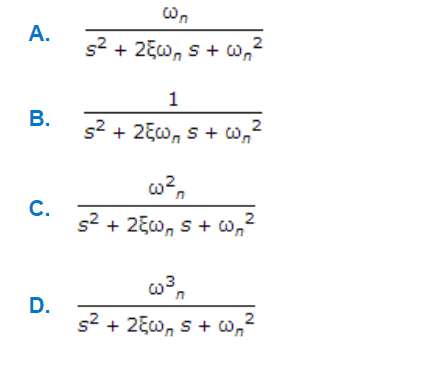
Post a Comment for "Damping Ratio Second Order System"